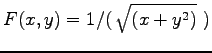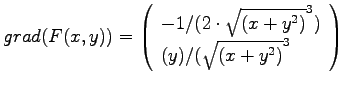SS 03 - Lösungen zur Prüfung 2, G, 20.Aug.2003

G   Ingenieurmathematik Prüfung 2 20.August2003
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Welches sind die Dimensionszahlen der beiden möglichen Produkte eines Vektors ``v'' der Länge ``n'' mit sich selbst: v*v' und v'*v

L:

1x1 Skalarprodukt und nxn dyadisches Produkt.

1b)

Geben sie alle Lösungen zur Gleichung $z^2 = i$.

L:

exp(j*pi/4), exp(j*5*pi/4)

1c)

Wozu dient im Zusammenhang mit der Faltung das ``zero padding'' (Anhängen von Nullen)?

L:

Um bei beiden Eingabe Folgen die Länge des Resultates der gewöhnlichen Faltung zu erreichen und diese damit auf eine zirkuläre Faltung zurückzuführen.

1d)

Nennen Sie zwei formale Bedingungen welche ein Function-m-File erfüllen muss, damit es von MATLAB als solches behandelt wird.

L:

Die erste (nicht-Kommentar-) Zeile muss mit derm Wort function beginnen
Der Funktionsname (direkt vor der Parameter-Klammer) muss mit dem Filenamen (ohne .m) übereinstimmen.

2)

Stellen Sie das Gleichungssystem auf für den Geradenfit $a \cdot x + b$ an die drei Punkte
$(-2 / p)$, $(0 / 0)$ und $(2 / q)$. (p und q sind noch nicht festgelegte Parameter, welche in den Gleichungen enthalten sein werden.)

L:

x = [-2 0 2]; y = [p 0 q]; M = [sx2 sx; sx 3] = [8 0; 0 3]
b = [2*q-2*p, p+q]'; [a,b] = M;

3)

Bestimmen Sie die Hesse'sche Normalform der Ebene durch die drei Punkte A(0/4/4) , B(0/7/0) , C(4/4/0) und bestimmen Sie die Durchstosspunkte der x- und z-Achsen durch diese Ebene.

L:

A = [0 4 4]'; B=[0 7 0]'; C=[4 4 0]'
n = cross(A-B,C-B), ne = n/norm(n), d = ne'*A
%n =[ 12 16 12]; ne = [ 0.5145 0.6860 0.5145]'; d= 4.8020
 xs = d/ne(1) ;  Sx = [ xs  0  0]'; ne'*Sx-d % ys = 9.333
 zs = d/ne(3) ;  Sz = [ 0 0 zs]' ;  ne'*Sz-d % zs = 9.333

4)

Suchen Sie die speziellen Permutationsmatrizen $Pl$ und $Pr$, so dass die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
$${ \left( \begin{array}{rrrr} d_4 & 0 & 0 & d_2 \\ 0 & 0 & 0& 0 \... ... c_1 & c_2 & c_3 & c_4 \\ d_1 & d_2 & d_3 & d_4 \end{array}\right) \cdot Pr }$$

L:

$${ Pl = \left( \begin{array}{rrrr} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0... ... \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array}\right) }$$

5)

Suchen Sie die drei Gesamt-Transformations-Matrizen, in homogenen Koordinaten der Ebene, welche das Rechteck A(0/0) B(8/0) C(8/4) D(0/4) in die drei übrigen Rechtecke transformiert, so dass die Umhüllung der vier Rechtecke das Quadrat (0/0) (0/12) (12/12) (12/0) bildet und die benachbarten Rechtecke sich nur berühren aber nicht überlappen.

L:

Rur = [0 8 8 0 0; 0 0 4 4 0; 1 1 1 1 1];
T1 = [1 0 -6; 0 1 -6; 0 0 1]; RTb = [0 1 6; -1 0 6; 0 0 1];
TT = RTb*T1    % TT=   [0 1 0; -1 0 12; 0 0 1]
R1 = TT*Rur, R2 = TT^2*Rur, R3=TT^3*Rur, hold on
plot(Rur(1,:),Rur(2,:),'k'); plot(R1(1,:),R1(2,:),'r'); 
plot(R2(1,:),R2(2,:),'g'); plot(R3(1,:),R3(2,:),'b');
axis([-1 13 -1 13]); axis square; hold off

6)

Geben Sie die (vektorwertige) Gradient-Funktion zur folgenden Funktion von zwei Variabeln an: $${ F(x,y) = 1/(\,\sqrt{(x+y^2)} ~ ) }$$

L:

$${ grad(F(x,y)) = \left( \begin{array}{lll} -1/(2\cdot \sqrt{(x+y^2)}^3) \\ (y)/( \sqrt{(x+y^2)}^3 \end{array}\right) }$$