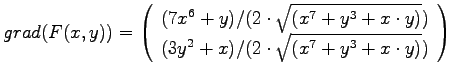SS 03 - Lösungen zur Prüfung 2, R-G-B-Y, 20.Aug.2003

R   Ingenieurmathematik Prüfung 2 20.August2003
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Geben Sie die Dimensionen der beiden Resultate der Mutliplikation einer nxm Rechtecksmatrix A mit sich selbst: A'*A und A*A'.

L:

A'*A ist mxm und A*A' ist nxn

1b)

Geben sie alle Lösungen zur Gleichung $z^4 -1 = 0$.

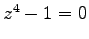L:

1, i, -1, -i

1c)

Welcher Unterschied besteht zwischen einer gewöhnlichen Faltung und einer zirkulären Faltung?

L:

Die Eingabe-Folgen müssen bei der zirkulären Faltung gleich sein und das Resultat hat dann auch dieselbe Länge. Bei der gewöhnlichen Faltung können sie verschieden lang sein und das Resultat hat die Länge $n1+n2-1$. Bei der immer wieder verschoben platzierten Folge der Kern-Funktion werden über den Rand hinausragende Werte am anderen Rand wieder (zyklisch) in die Berechnungs-Tabelle eingefügt.

1d)

Wie ermöglicht man die simultane Rückgabe von zwei verschiedenartigen Resultat-Grössen durch eine Matlab-Funktion?

L:

Mit dem Aufruf [Res1, Res2] = funktion(Parameter)

2)

Stellen Sie das Gleichungssystem auf für den Geradenfit $a \cdot x + b$ an die drei Punkte
$(-1 / p)$, $(0 / 0)$ und $(2 / q)$. (p und q sind noch nicht festgelegte Parameter, welche in den Gleichungen enthalten sein werden.)

L:

x = [-1 0 2]; y = [p 0 q]; M = [sx2 sx; sx 3] = [5 1; 1 3]
b = [2*q-p, p+q]'; [a,b] = M;

3)

Bestimmen Sie die Hesse'sche Normalform der Ebene durch die drei Punkte A(14/0/0) , B(8/8/0) , C(8/0/8) und bestimmen Sie die Durchstosspunkte der y- und z-Achsen durch diese Ebene.

L:

A = [14 0 0]'; B=[8 8 0]'; C=[8 0 8]'
n = cross(B-A,C-A), ne = n/norm(n), d = ne'*A
%n =[ 64 48 48]; ne = [ 0.6860 0.5145 0.5145]'; d= 9.6039
 ys = d/ne(2) ;  Sy = [ 0 ys 0]' ne'*Sy-d % ys = 18.6667 
 zs = d/ne(3) ;  Sz = [ 0 0 zs]' ne'*Sz-d % zs = 18.6667 

4)

Suchen Sie die speziellen Permutationsmatrizen $Pl$ und $Pr$, so dass die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
$${ \left( \begin{array}{rrrr} 0 & a_3 & 0 & a_1 \\ 0 & 0 & 0& 0 ... ... c_1 & c_2 & c_3 & c_4 \\ d_1 & d_2 & d_3 & d_4 \end{array}\right) \cdot Pr }$$

L:

$${ Pl = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0... ... 1 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) }$$

5)

Suchen Sie die drei Gesamt-Transformations-Matrizen, in homogenen Koordinaten der Ebene, welche das Rechteck A(0/0) B(8/0) C(8/2) D(0/2) in die drei übrigen Rechtecke transformiert, so dass die Umhüllung der vier Rechtecke das Quadrat (0/0) (0/10) (10/10) (10/0) bildet und die benachbarten Rechtecke sich nur berühren aber nicht überlappen.

L:

Rur = [0 8 8 0 0; 0 0 2 2 0; 1 1 1 1 1];
T1 = [1 0 -5; 0 1 -5; 0 0 1]; RTb = [0 1 5; -1 0 5; 0 0 1];
TT = RTb*T1    % TT=   [0 1 0; -1 0 12; 0 0 1]
R1 = TT*Rur, R2 = TT^2*Rur, R3=TT^3*Rur, hold on
plot(Rur(1,:),Rur(2,:),'k'); plot(R1(1,:),R1(2,:),'r'); 
plot(R2(1,:),R2(2,:),'g'); plot(R3(1,:),R3(2,:),'b');
axis([-1 11 -1 11]); axis square; hold off

6)

Geben Sie die (vektorwertige) Gradient-Funktion zur folgenden Funktion von zwei Variabeln an:
$${ F(x,y) = \sqrt{(x^7+y^3+x\cdot y)} }$$

L:

$${ grad(F(x,y)) = \left( \begin{array}{lll} (7x^6+y)/(2\cdot \sqr... ...dot y)}) \\ (3y^2+x)/(2\cdot \sqrt{(x^7+y^3+x\cdot y)}) \end{array}\right) }$$