










Nächste Seite: FS 09 - Lösungen
Aufwärts: Frühjahrssemester 2009
Vorherige Seite: FS 09 - Prüfung
Inhalt
Y
Ingenieurmathematik Prüfung 2
12.Mai2009
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe,
40 Pt. = N.6.
- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- 1a)
- Geben Sie eine
der beiden Quadratwurzeln von
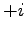 an.
an.
- 1b)
- Mit M = [6 3 0; 0 3 0] sind die Koordinatenpaare
der 3 Ecken eines Dreiecks definiert (obere Zeile x, untere y).
Mit welchen MATLAB-Befehlen erreichen Sie, dass dieses Dreieck
mit allen 3 Seiten
unverzerrt gezeichnet wird?
- 1c)
- Schreiben Sie ein Beispiel auf für eine 2x2 orthogonale Matrix,
welche verschieden ist von der Einheitsmatrix.
- 1d)
- Welches Element wird bei der Pivotkontolle für die
Spalte 'k' darauf geprüft, ob es nicht Null ist?
- 2)
- Geben Sie das MATLAB-Skript an zum Zeichnen einer linksgängigen
Schraubenlinie mit der x-Achse als Schrauben-Achse, dem Anfangs-Punkt
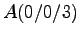 , dem Endpunkt
, dem Endpunkt 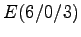 und 4 Umgängen.
und 4 Umgängen.
- 3)
- Geben Sie zwei komplexe Zahlenfolgen
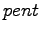 und
und
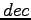 an, welche beim Zeichnen mit plot(pent) eine
geschlossene reguläre Fünfeck-Figur und mit
plot(dec) ein vollständiges Zehn-Eck ergeben.
Beide Figuren müssen im Einheitskreis einbeschrieben sein
und beide müssen eine Ecke
bei 90 Grad d.h. bei
an, welche beim Zeichnen mit plot(pent) eine
geschlossene reguläre Fünfeck-Figur und mit
plot(dec) ein vollständiges Zehn-Eck ergeben.
Beide Figuren müssen im Einheitskreis einbeschrieben sein
und beide müssen eine Ecke
bei 90 Grad d.h. bei 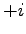 haben.
haben.
- 4)
- Der Quader ABCD EFGH
Der Quader ABCD EFGH
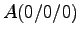
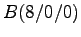
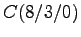
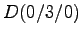
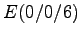
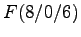
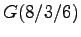
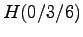
wird von zwei zueinander parallelen Ebenen
geschnitten: 1. Ebene f durch 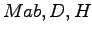
2. Ebene g durch 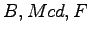
wobei 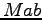 der Mittelpunkt der Strecke
der Mittelpunkt der Strecke 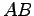 ist, und
ist, und
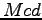 der Mittelpunkt der Strecke
der Mittelpunkt der Strecke 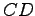 .
.
Geben Sie die Hesse'sche Normalformen dieser
beiden Ebenen an und berechnen Sie die Durchstosspunkte
der Geraden 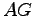 durch diese beiden Ebenen.
durch diese beiden Ebenen.
Die Tatsache, dass die beiden Ebenen f und g zueinander
parallel sind,
müssen Sie nicht nachprüfen.
- 5)
- Erstellen Sie eine MATLAB Funktion, welche eine
quadratische Matrix als Eingabe erhält und daraus
(durch Bearbeitung von Einzel-Elementen im Innern einer
Doppelschleife) eine antisymmetrische Matrix erstellt,
bei welcher die Werte rechts- bzw. oberhalb der Diagonalen
mit der eingegebenen Matrix identisch sind.
- 6)
- Geben Sie die Teilmatrizen und die Gesamt-Transformations-Matrix
an für die 2D homogene Koordinatentransformation, welche
das gleichseitige Dreieck ABC (
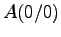 ,
, 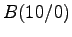 ,
,
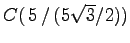 )
an der Geraden
)
an der Geraden
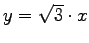 spiegelt.
Geben Sie auch die Ecken des
transformierten Dreiecks an.
spiegelt.
Geben Sie auch die Ecken des
transformierten Dreiecks an.












Nächste Seite: FS 09 - Lösungen
Aufwärts: Frühjahrssemester 2009
Vorherige Seite: FS 09 - Prüfung
Inhalt
2012-03-21
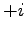 an.
an.
