- 1a)
- Warum ist die Formel der Kramer'schen Regel für die praktische
Lösung von grösseren linearen Gleichungssystemen ungeeignet?
- L)
- Weil der Aufwand zur Auswertung der Formel enorm stark ansteigt
(
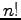 ), viel viel stärker als z. B. bei der Gauss-Elimination (
), viel viel stärker als z. B. bei der Gauss-Elimination (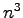 ).
).
- 1b)
- Bestimmen Sie die zwei Resultate: Skalarprodukt der Vektoren
![$v = [-1 ~ 1]'$](img1082.png) und
und ![$w = [1 ~ 1]'$](img1083.png) , sowie das Produkt der komplexen Zahlen
, sowie das Produkt der komplexen Zahlen
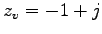 und
und 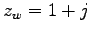 . Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
. Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
- L)
-1*1 + 1*1 = 0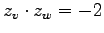
- 1c)
- Wie heissen die MATLAB Funktionen zur Berechung des
grössten gemeinsamen Teilers und zur Bestimmung des kleinsten gemeinsamen
Vielfachen?
- L)
gcd(z1,z2) , lcm(z1,z2)- 1d)
- Wieviele Begegnungen gibt es bei einer einfachen Turnier-Runde (keine
Hin- und Rückspiele) von n Teilnehmern?
- L)
- n*(n-1)/2
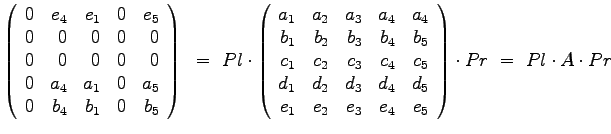
Pl3 = [0 0 0 0 1; 0 0 0 0 0; 0 0 0 0 0; 1 0 0 0 0; 0 1 0 0 0]
Pr3 = [0 0 1 0 0; 0 0 0 0 0; 0 0 0 0 0; 0 1 0 0 0; 0 0 0 0 1]
M= [6 6 4]'
en = [ 0 -0.6 0.8]
Distanzen: A,B: d=0.4 , C: d= -5, D: d=5
Geben Sie auch ein MATLAB-Skript an, das diese Transformation in homogenen Koordinaten durchführt und das Urbild und Bild in eine gemeinsame Grafik einzeichnet.
T1 = [1 0 -6; 0 1 -4;0 0 1]; T2 = [0 1 0; -1 0 0 ; 0 0 1]; T3 = [1 0 6; 0 1 4;0 0 1]; TT = T3*T2*T1 % =[0 1 2; -1 0 10 ; 0 0 1]; Q = [6 12 12 6 6; -2 -2 4 4 -2; 1 1 1 1 1]; QT = TT*Q; plot(Q(1,:),Q(2,:)); hold on; plot(QT(1,:),QT(2,:),'r'); axis([-15 15 -15 15]); axis square; hold off
w=(0:0.02:5)*2*pi; x= 4*cos(w); z= -4*sin(w); yr= w*0.6/2/pi; yl = -yr; clf; plot3(x,yr,z); hold on; plot3(x,yl,z,'m'); axis equal; hold off
