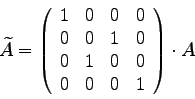- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- 1a)
- Geben Sie vier MATLAB Standardfunktionen an, welche einen komplexen
Eingabewert und einen reellen Ausgabewert haben.
- L:
- real(), imag(), abs(), angle()
- 1b)
- Wieviele Nullen hat eine nxn Tridiagonalmatrix mindestens?
- L:
-
 Matrix minus Diagonale minus zwei Nebendiagonalen.
Matrix minus Diagonale minus zwei Nebendiagonalen.
- 1c)
- Wie lautet der MATLAB-Befehl, um dem mit plot3 zu zeichnenden Bereich
eine Würfel-Form vorzuschreiben?
- L:
- axis([-d d -d d -d d]); axis square
- 1d)
- Wie nennt man die beiden wichtigsten Gleichungs-Ansätze,
welche für das Lösen von Fit-Problemen angewendet werden.
- L:
- Normalengleichungen und Fehlergleichungen
- 2)
- Ein Windschutzzelt hat einen Grundriss in der Form
eines rechtwinkligen Dreiecks. Die Bodenpukte der Verspannung sind
C=(0/0), A=(6/0), und B=(0/8). In der Mitte der Hypothenuse ist ein 2 Meter
hoher vertikaler Stützpfosten zum Punkt S. Berechnen Sie den
Winkel zwischen den zwei Dreiecksflächen CAS und CBS.
- L:
C=[0 0 0]'; A=[6 0 0]'; B=[0 8 0]'; S=(A+B)/2+[0 0 2]';
na=cross(A-C,S-C); nb=cross(S-C,B-C); coswi = na'*nb/norm(na)/norm(nb);
wi = acos(coswi)*180/pi ,na ,nb % wi = 41.9088 Grad
% na = [0 -12 24]' , nb = [-16 0 24]'
- 3)
- Schreiben Sie ein Matlab-Skript, das dieselbe Wirkung hat, wie die
Multiplikation von links mit der unten angegebenen Matrix. Das Skript soll
also eine beliebige 4x4 Matrix
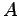 in eine
entsprechende Matrix
in eine
entsprechende Matrix 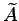 umforman.
umforman.
- L:
A=[11 12 13 14; 21 22 23 24; 31 32 33 34; 41 42 43 44];
idar=[1 3 2 4]; Atr = A;
for k=1:4;
Atr(k,:)=A(idar(k),:);
end; Atr
- 4)
- Ein (rechtwinkliger) Quader hat die Seitenlängen 8, 6 und 3
in x,y und z-Richtung. Die Ecken werden in der unteren Ebene
im Gegenuhrzeigersinn mit ABCD bezeichet und korrespondierend in der oberen
mit EFGH. A sei im Nullpunkt. Bestimmen Sie die Ebenengleichung
in der Hesse'schen Normalform für die Ebene durch die drei Punkte
F,C,H, sowie der Ebenen die dazu parallel sind und durch A und durch G
gehen.
- L:
A=[0 0 0]'; B=[8 0 0]'; C=[8 6 0]'; D=[0 6 0]';
E=[0 0 3]'; F=[8 0 3]'; G=[8 6 3]'; H=[0 6 3]';
na=cross(H-C,F-C); ne=na/norm(na)
ne'*F, ne'*C, ne'*H, ne'*G
% ne = [0.3180 0.4240 0.8480]'
% Ebenen: ne'*OP - 5.0880 = 0 ; ne'*OP = 0 ; ne'*OP - 7.6320 = 0 ;
- 5)
- Suchen Sie alle Teil-Transformationsmatrizen,
die Gesamt-Transformations-Matrix und die abgebildete Figur
in homogenen Koordinaten der Ebene, welche die ``L'' -Figur
(4/2) (4/0) (5/0)
an der Geraden
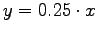 spiegeln.
spiegeln.
- L:
Lur = [4 4 5; 2 0 0; 1 1 1]; w = atan(0.25);
Mr1 = [cos(-w) -sin(-w) 0; sin(-w) cos(-w) 0; 0 0 1]
Mirr = [1 0 0; 0 -1 0; 0 0 1]
Mr2 = [cos(w) -sin(w) 0; sin(w) cos(w) 0; 0 0 1]
Mt = Mr2*Mirr*Mr1 , Lb = Mt*Lur
plot(Lur(1,:),Lur(2,:)); hold on; plot(Lb(1,:),Lb(2,:),'r')
axis([-1 9 -1 9]); axis square; plot([0 10],[0 2.5]); hold off
- 6)
- Geben Sie die Funktion des totalen Differentials
 an für die
Funktion
an für die
Funktion
 .
.
- L:
-
 Matrix minus Diagonale minus zwei Nebendiagonalen.
Matrix minus Diagonale minus zwei Nebendiagonalen.