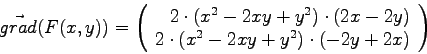


Nächste Seite: Sommersemester 2005
Aufwärts: Wintersemester 2004/05
Vorherige Seite: WS 04/05 - Prüfung
Inhalt
Ingenieurmathematik Prüfung 2
2.März2005
Zeit 90 Minuten, Reihenfolge beliebig, Zwischenresultate obligatorisch,
Max.6*8 P., 40 P. = N.6.
- 1)
- Verständnisfragen: Es werden nur ganz
kurze Antworten erwartet.
- 1a)
- Mit welchem Befehl zeichnet man mit MATLAB die durch die Vektoren x und y
definierte Punkteschar als violettrote diagonale Kreuze?
- L:
- plot(x,y,'mx')
- 1b)
- Wie gross ist die Länge der Resultatfolge bei einer gewöhnlichen
Faltung der beiden Folgen a und b , welche je die Länge n haben,
und welche Länge hat eine zirkuläre Faltung von a mit b?
- L:
- 2*n-1 ; n
- 1c)
- Welches ist der maximal mögliche Rang einer breiten Rechtecksmatrix
der Dimension n x m?
- L:
- Antwort: n, die kleinere der zwei Dimensionen
- 1d)
- In einer DFT einer Folge der Länge 80 sind die (komplexen)
Koeffizienten
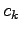 mit
mit 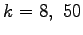 durch Übertragungsfehler
verlorengegangen. Wie können diese aus den anderen, intakt
gebliebenen Koeffizienten rekonstruiert werden?
durch Übertragungsfehler
verlorengegangen. Wie können diese aus den anderen, intakt
gebliebenen Koeffizienten rekonstruiert werden?
- L:
-
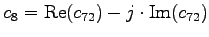
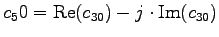
- 2)
- Finden Sie durch Überlegen je die Inversen Matrizen zu den unten angegebenen
und beschreiben Sie Ihre Lösungs-Idee.
- L:
- Die erste Matrix ist eine Rotation um
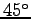 ,
deren Inverse also eine Rotation um
,
deren Inverse also eine Rotation um
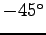 . Die zweite Matrix
ist eine zyklische scroll-down Matrix, die dazu Inverse also eine
scroll-up Matrix.
. Die zweite Matrix
ist eine zyklische scroll-down Matrix, die dazu Inverse also eine
scroll-up Matrix.
- 3)
- Schreiben Sie ein Programm in Matlab-Code
zum Erstellen einer nxn antisymmetrischen Matrix
('n' vorgegebener Parameter), welche in den von Null verschiedenen Elementen
Werte enthält, deren Betrag dem Abstand von der Diagonalen entspricht, und
deren Elemente im oberen Dreiecks-Teil positiv sind.
- L:
-
A=zeros(n);
for zei = 1:n
for spa = 1:n
A(zei,spa) = spa - zei;
end
end
- 4)
- Geben Sie die Transformationsmatrizen in homogenen Koordinaten an,
für die Transformationen R) und S), sowie die Koordinaten der
transformierten Punkte. Es sind jeweils
die Gesamt-Transformation und die zugehörigen Teiltransformationen
anzugeben. Bei R) wird das Quadrat A
 , B
, B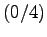 C
C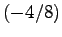 D
D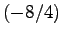 um den Punkt B um den Winkel
um den Punkt B um den Winkel
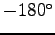 gedreht.
Bei S) wird dasselbe Quadrat an der y-Achse gespiegelt.
Zeigen Sie, dass die beiden Bildquadrate übereinander liegen indem Sie
die zusammenpassenden Paare von Bildpunkten suchen.
gedreht.
Bei S) wird dasselbe Quadrat an der y-Achse gespiegelt.
Zeigen Sie, dass die beiden Bildquadrate übereinander liegen indem Sie
die zusammenpassenden Paare von Bildpunkten suchen.
- L:
-
Spiegelung S):
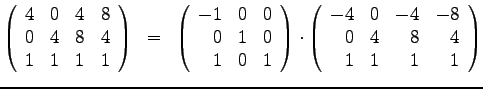
Vertikaltranslation B zu O, dann Drehung, dann Ruecktranslation:

Gesamt-Transformation R):
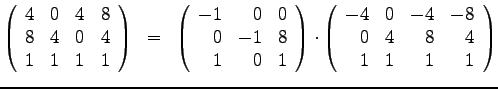
Vergleich S)-R): Ats = Ctr, Bts = Btr, Cts = Atr, Dts = Dtr
- 5)
- Berechnen Sie ``von Hand'', unter Angabe der
zu summierenden Tabelle
sowohl die zirkuläre Faltung als auch die
gewöhnliche Faltung der Folge [1 1 2 1 1] mit sich selbst.
- L:
-
![$
\begin{array}[t]{rrrrrrrrr}
1 & 1 & 2 & 1 & 1\\
& 1 & 1 & 2 & 1 & 1 \\
& &...
...2 & 1 & 1 & 1 & 1\\
1 & 2 & 1 & 1 & 1\\
\hline
7 & 7 & 7 & 7 & 8
\end{array}$](img731.png)
- 6)
- Bestimmen Sie
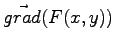 für die Funktion
für die Funktion
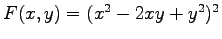 .
.
- L:
-












Nächste Seite: Sommersemester 2005
Aufwärts: Wintersemester 2004/05
Vorherige Seite: WS 04/05 - Prüfung
Inhalt
2012-03-21
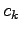 mit
mit 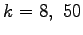 durch Übertragungsfehler
verlorengegangen. Wie können diese aus den anderen, intakt
gebliebenen Koeffizienten rekonstruiert werden?
durch Übertragungsfehler
verlorengegangen. Wie können diese aus den anderen, intakt
gebliebenen Koeffizienten rekonstruiert werden?
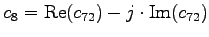
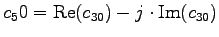
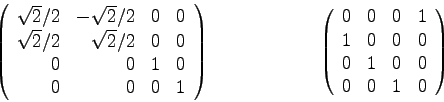

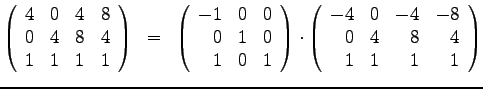

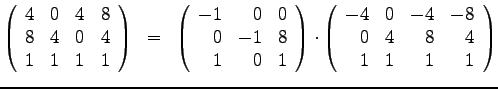
![$
\begin{array}[t]{rrrrrrrrr}
1 & 1 & 2 & 1 & 1\\
& 1 & 1 & 2 & 1 & 1 \\
& &...
...2 & 1 & 1 & 1 & 1\\
1 & 2 & 1 & 1 & 1\\
\hline
7 & 7 & 7 & 7 & 8
\end{array}$](img731.png)