HS 10/11 - Lösungen zur Prüfung E 2, 7. Dez. 2010

Lösungen zur Prüfung 2 7.Dez.2010
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Zerlegen Sie die Matrix M = [2 4 ; 1 3] in eine Summe aus einer symmetrischen, (S) und einer antisymmetrischen (A) Matrix, d.h. geben Sie S und A an, so dass M = S+A gilt.

L1a)

S=[2 2.5 ; 2.5 3], A = [0 1.5 ; -1.5 0]

1b)

Geben Sie die noch aubzuarbeitenden Index-Paare (= Orte an denen noch Nullen erzeugt werden müssen) bei der Gauss-Elimination an, für eine 4x4 Matrix, nachdem die erste Spalte bereits vollständig abgearbeitet wurde, so dass nun mit der zweiten Spalte begonnen wird.

L1b)

(3,2), (4,2) , (4,3)

1c)

Bestimmen Sie die Inverse 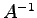$A^{-1}$ der untenstehenden Matrix $A$ unter Verwendung der Angabe, dass die gegebene Matrix orthogonal ist. $A = \left( \begin{array}{rrr} 0 & -1 & 0\\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} \right)$

L1c)

$A^{-1} = A^T$

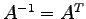
1d)

Bestimmen Sie den Wert q im Vektor v = [1 ; q ; 2] damit dieser zum Vektor u = [6 ; 3 ; -3] orthogonal wird.

1d)

q=0: 6*1 + 3*q-2*3 = 0

2)

Die aufeinanderfolgenden Potenzen $z,~z^2,~ z^3, \ldots z^k$ der komplexen Zahl $z = 1.2 \cdot \exp(- i \cdot \pi/3 )$ bilden eine ``eckige'' logarithmische Spirale.
Bestimmen Sie die möglichst kleinen Werte $k_1$ und $k_2$ von k, und dann auch die Werte von $z^{(k_1)}$ und $z^{(k_2)}$, so dass $z^{(k_1)}$ eine negative reelle Zahl und $z^{(k_2)}$ eine positive relle Zahl ist.

L2)

Aus $z^k = (1.2)^k \cdot \exp(- i \cdot k \cdot \pi/3 )$ ergibt sich für negativ reell $k \cdot \pi/3 = \pi$, also $k_1 = 3$ $z_1 = -1.728$ und für positiv reell $k \cdot \pi/3 =2 \pi$ also $k_2 = 6$ $z_2 = +2.986$

3)

Eine rechtsgängige Schraubenlinie startet im Punkt $(0/0/0)$ und endet nach einem Viertel Umgang im Punkt $(6/{-6}/4)$. Die Achse ist parallel zu z-Achse. Bestimmen Sie die x-y-Achsenposition, den Startwinkel und den Radius dieser Schraubenlinie aus der Grundriss-Zeichnung, in welcher die Linie als Viertelkreis erscheint.
Bestimmen Sie anschliessend noch die fehlenden Parameter zur Beschreibung dieser Linie.

L3)

Die Achse befindet sich bei B = (6/0) in der rechten oberen Ecke des Quadrates A = 0/0; B = 6/0; C = 6/-6; D = 0/-6 in welchem der Viertelkreis mit Radius 6 von A nach C naeher an der Ecke D vorbei verläuft.
Der Startwinkel ist pi, die Ganghoehe 4*2 = 8.

t = 0:0.02:pi/2; 
 x = 6*cos(t+pi) + 6;  
y = 6*sin(t + pi) + 0; 
z = t*8/2/pi;
axis([0 6 -6 0 0 6])
axis square
box on

4)

Im Quader ABCD-EFGH $A= (0/0/0)$, $B= (4/0/0)$, $C= (4/3/0)$, $D= (0/3/0)$,
$E= (0/0/3.2)$, $F= (4/0/3.2)$, $G= (4/3/3.2)$, $H= (0/3/3.2)$, wird zuerst eine Ebene durch die Punkte B, D, G gelegt, deren Hesse'sche Normalform zu bestimmen ist. Zeigen Sie durch Berechnen der Abstände, dass die Ebene durch die Punkte A,F,H parallel zur ersten ist, und geben Sie auch noch die Hesse'sche Normalform dieser Parallel-Ebene an.

L4)

A = [ 0 0 0]' ,  B= [4 0 0]' ,  C= [4 3 0]' ,  D= [0 3 0]'     
 E= [0 0 3.2]' ,  F= [4 0 3.2]' ,  G= [4 3 3.2]' ,  H= [0 3 3.2]'   
u = D-B , v = G - B
N = cross(u,v)     % [9.6 12.8 -12.0]
lN = norm(N)      %  20
en = N/lN          %  [0.48 0.64 -0.6]  
dkrit = en'*B     %  1.92
% 
dA = en'*A - dkrit   %  alle -1.92
dF = en'*F - dkrit
dH = en'*H - dkrit
%  en2 identisch  [0.48 0.64 -0.6] 
dkrit2 = en'*A  = 0
%  en2'*OP -0 =0

5)

Das Dreieck ABC $A=(2/0)$, $B=(6/0)$, $C=(4/3)$ soll mit homogener Koordinatentransformation um seinen Schwerpunkt um 180 Grad gedreht werden.
Geben Sie alle Teil-Transformations-Matrizen in homogenen Koordinaten der Ebene an, die bei dieset Abbildung angewandt werden, sowie die Gesamt-Transformationsmatrix dieser Abbildung.
Die Gesamt-Transformationsmatrix soll anschliessend quadriert werden.
Die Bildkoordinaten nach der Drehung um den Schwerpunkt sind ebenfalls anzugeben.

L4)

 A = [2 0 1]'; B = [6 0 1]'; C = [4 3 1]'
Dur = [A B C A];
Sp = [(A(1:2)+B(1:2)+C(1:2))/3 ; 1 ]
Tzen = [ 1 0 -Sp(1) ; 0 1 -Sp(2); 0 0 1]
R180 = [-1 0 0 ; 0 -1 0 ; 0 0 1]
Tbk = [ 1 0 Sp(1) ; 0 1 Sp(2); 0 0 1]
Ttot = Tbk * R180 * Tzen
Dbil = Ttot * Dur
Tdblrot = Ttot^2
figure(1)
clf
plot(Dur(1,:),Dur(2,:),'g')
hold on
plot(Dbil(1,:),Dbil(2,:),'r')
axis equal
hold off

6)

zvec sei der Vektor aller komplexen Lösungen der Gleichung $z^4 = i$. Suchen Sie eine komplexe Zahl zr, welche zvec beim Multiplizieren so rotiert, dass mindestens einer der Werte aus dem mit zr multiplizierten Vektor zvec, also aus zvmod = zr*zvec eine reelle Zahl ist.

L6)

Die Lösungen von $z^4 = i$ sind exp(i*(pi/4 + k*pi/2)).
um die Lösung für k=0 reell zu machen braucht es eine Multiplikation um -pi/4 also eine Multiplikation mit zr = exp(-i*pi/4).