- 1a)
- Beim Matrizenprodukt P=A*B*C*D sind die Dimensionen
von A (6x5), von B(wx5),
von C (5xu) und von D(6x6). Bestimmen Sie w und u, so dass das Produkt legal ist, und geben Sie die Dimensionen von P an - L1a)
- w = 5, u = 6, P = (6x6)
- 1b)
- Geben Sie zwei komplexe Zahlen z1 und z2 an, so dass eine beliebige Zahl z
durch Multiplizieren mit z1 um 60 Grad und mit z2 um 180 Grad in
der Gauss'schen Zahlenebene gedreht wird (bei gleichbleibendem Betrag).
z1, z2 können in beliebiger Form angegeben werden.
- L1b)
- z1 = exp(i*pi/3), z2 = -1
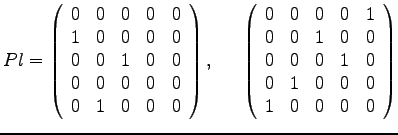
- 1c)
- Bestimmen Sie den Wert
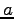 in der
untenstehenden Eliminationsmatrix
in der
untenstehenden Eliminationsmatrix 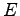 , so dass
, so dass 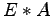 eine Rechtsdreiecks-Matrix ist. Geben Sie auch diese Matrix
eine Rechtsdreiecks-Matrix ist. Geben Sie auch diese Matrix  an!
an!

- L1c)
- a = -1

- 1d)
- Geben Sie zum Vektor
v = [2 ; 3]die beiden Produkte (Skalarprodukt)s = v'*vund (dyadisches Produkt)Mv = v*v'an! - L1d)
-
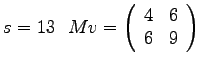

t = 0:pi/100:6*pi ; gh = 2; x = 2*sqrt(2)*cos(t + 5*pi/4) + 0 y = 2*sqrt(2)*sin(t + 5*pi/4) + 0 z = t*gh/(2*pi) plot3(x,y,z) axis equal hold on plot3([-2 -2 -2 -2 ],[-2 -2 -2 -2],[0 2 4 6],'ro') % + xz Ebene bei t+5*pi/4 = 2*pi, also bei t=3*pi/4 xe = 2*sqrt(2), ye = 0, ze = 3*pi/4*gh/(2*pi) % ze = 0.75 plot3([xe,xe,xe],[ye,ye,ye],[ze ze+2 ze+4],'mo') hold off
werden zuerst die Mittelpunkte MET und MWT der Kanten ET und WT bestimmt. Dann soll die Hesse'sche Normalform der Ebene durch die Punkte S, MET, MWT bestimmt werden.
Berechnen Sie damit den Abstand der Punkte T, N und
N = [0 2 0]'; E = [2 0 0]'; S = [0 -2 0]';
W = [-2 0 0]'; T = [0 0 2]'; B = [0 0 -2]';
MWT = (W+T)/2,MET = (E+T)/2
u = MWT-S, v = MET - S
No = cross(u,v)
en = No/norm(No)
dkrit = en'*S
dT = en'*T - dkrit
dN = en'*N - dkrit
MH = [0 0 1]'
dMH = en'*MH -dkrit
Oc = [S T N B S E T W B E N W S];
Cl = [S MWT MET S]
plot3(Oc(1,:),Oc(2,:),Oc(3,:),'k')
hold on ; axis equal
plot3(Cl(1,:),Cl(2,:),Cl(3,:),'r')
hold off
view(12,8)
MWT =
-1
0
1
MET =
1
0
1
u =
-1
2
1
v =
1
2
1
No =
0
2
-4
en =
0
0.4472
-0.8944
dkrit =
-0.8944
dT =
-0.8944
dN =
1.7889
MH =
0
0
1
dMH =
0
Anschiessend ist das gedrehte Quadrat noch an der x-Achse zu spiegeln.
Geben Sie alle Teil-Transformations-Matrizen fuer diese Abbildungen in homogenen Koordinaten der Ebene an, sowie die Endkoordinaten der Eckpunkte und die Gesamt-Transformationsmatrix dieser Abbildungs-Abfolge.
Es werden in konkreten Zahlenwerten angegebene Matrizen und Vektoren (bzw. Koordinatenpaare) verlangt.
Qi = [3 5 5 3 ; 0 0 2 2 ; 1 1 1 1 ]
Tz = [1 0 -5; 0 1 0; 0 0 1]
Tb = [1 0 5; 0 1 0; 0 0 1]
R = [-1 0 0; 0 -1 0 ; 0 0 1]
M = [1 0 0; 0 -1 0 ; 0 0 1]
Ttot = M*Tb*R*Tz
Qz = Tz*Qi
Qzr = R*Qz
Qr = Tb * Qzr
Qf = M*Qr
stdhcaxis
plothclin(Qi,'g') ; plothclin(Qz,'b')
plothclin(Qzr,'m') ; plothclin(Qr,'r')
plothclin(Qf,'k') ; hold off
Qi =
3 5 5 3
0 0 2 2
1 1 1 1
Tz =
1 0 -5
0 1 0
0 0 1
Tb =
1 0 5
0 1 0
0 0 1
R =
-1 0 0
0 -1 0
0 0 1
M =
1 0 0
0 -1 0
0 0 1
Ttot =
-1 0 10
0 1 0
0 0 1
Qz =
-2 0 0 -2
0 0 2 2
1 1 1 1
Qzr =
2 0 0 2
0 0 -2 -2
1 1 1 1
Qr =
7 5 5 7
0 0 -2 -2
1 1 1 1
Qf =
7 5 5 7
0 0 2 2
1 1 1 1
a) zwischen den Vektoren B-MDH und B-H und b) zwischen den Vektoren B-MDH und B-G
A=[0 0 0]', B=[2 0 0]',
C=[2 2 0]', D=[0 2 0]',
E=[0 0 2]', F=[2 0 2]',
G=[2 2 2]', H=[0 2 2]',
MDH = (D+H)/2
uab = MDH - B
va = H - B
vb = G - B
wa = acosd(uab'*va/norm(uab)/norm(va))
wb = acosd(uab'*vb/norm(uab)/norm(vb))
MDH =
0
2
1
uab =
-2
2
1
va =
-2
2
2
vb =
0
2
2
wa =
15.7932
wb =
45.0000
