- 1a)
- Wieviele Nullen besitzt eine Rechts-Dreiecksmatrix der Dimension nxn mindestens?
- L1a)
-
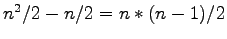
- 1b)
- Geben Sie je die 4. Potenzen (also
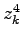 ) an für die beiden Zahlen:
) an für die beiden Zahlen:
 ,
,

- L1b)
-
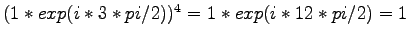
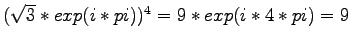
- 1c)
- Wie erreicht man in MATLAB, dass der nachfolgende plot-Aufruf
in dasselbe Bild gezeichnet wird?
- L1c)
- hold on
- 1d)
Geben Sie die Inverse 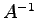 zur nebenstehenden Matrix
zur nebenstehenden Matrix 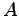 an.
Verwenden Sie dazu die Information , dass A orthogonal ist.
an.
Verwenden Sie dazu die Information , dass A orthogonal ist.

Welche möglichst tiefe Potenz, also welches möglichst kleine
a) eine negative reelle Zahl , b) eine positive relle Zahl?
Geben Sie die zu a) und b) gehörenden Zahlen an!
für negativ reel muss w = pi sein, also k1 = 3,
für positiv reel muss w = 2*pi sein, also k1 = 6,
Bestimmen Sie die Parameter dieser Schraubenlinie und geben Sie ein MATLAB-Skript an, mit dem diese Linie gezeichnet wird. Hinweis: Zeichnen Sie einen Grundriss dieser Figur zur einfacheren Bestimmung der Achsenposition und des Radius.
n=1/4; w = (0:0.01:n)*2*pi; h = 2/n; r = 8; w0 = -pi/2; z = w*h/(2*pi); x = r*cos(w+w0); y = 8+r*sin(w+w0); plot3(x,y,z) box on axis equal view (-24,28)
Gesucht ist zuerst die Geradengleichung der Trägergeraden zur Seite AB in Hesse'scher Normalform.
Zusätzlich ist noch die Hesse'sche Normalform gesucht für die Trägergerade zur Seite CD (Die Punkte C, D müssen dazu nicht bestimmt werden.)
Hinweis: in der Ebene hat der zum Vektor
v = [v1 v2]' senkrechte
Vektor w die Komponenten w = [v2 -v1]'.
% Vektor in (auf) Gerade AB ist B-A A = [0 4]' ; B = [3 0]'; AB = B - A % = [3 -4]' % N aus AB durch Vertauschen und 1 Komponente Vozeichen aendern N = [4 3]' % nicht Verlangt N = AE N = BC C = B+N ; D = A+N ; % C= [4 7]' ; D = [7 3]'; en = N/norm(N) % = ¨[4 3]'/5 = [0.8 0.6]' dkrit = en'*A % = 2.4 dBtst = en'*B - dkrit % Gerade durch C,D enp = en % dkrit um 5 groesser dkritp = 7.4 dCtst = enp'*C - dkritp dDtst = enp'*D - dkritp
Bestimmen Sie auch die Koordinaten aller transformierten Ecken!
Qori = [2 7 7 2 2; 0 0 -3 -3 0; 1 1 1 1 1]; Tz = [1 0 -2; 0 1 0; 0 0 1] , Tbk = [1 0 2; 0 1 0; 0 0 1] R = [0 -1 0; 1 0 0; 0 0 1] Tt = Tbk * R * Tz Qn = Tt * Qori plot(Qori(1,:),Qori(2,:)) hold on axis equal plot(Qn(1,:),Qn(2,:),'r') hold off
Das Gleichungssystem, bei welchem alle 3 partiellen Ableitungen von
% 3 * x^2 + 2 * y^2 +lam * ( x - 3* y - 2) % dpL/dpx = 6*x + lam = 0 % dpL/dpy = 4*y - 3* lam = 0 % dpL/dplam = x - 3* y - 2 = 0 M = [4 0 1 ; 0 10 -2 ; 1 -2 0 ] b = [0 0 5]' xsol = M\b
