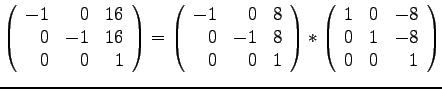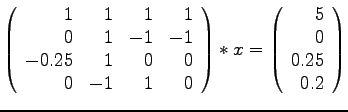


Nächste Seite: SS 2001 - Nachprüfung
Aufwärts: Sommersemester 2001
Vorherige Seite: Sommersemester 2001
Inhalt
A/B
Ingenieurmathematik Prüfung 1
26.Juni2001
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe,
40 Pt. = N.6.
- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- A/B 1a)
- Wieviele Zahlen sind notwendig zu einer
vollständigen Definition einer nxm Matrix.
- L:
- Die
 in der Matrix enthaltenen Zahlen plus die
2 Dimensionszahlen n und m.
in der Matrix enthaltenen Zahlen plus die
2 Dimensionszahlen n und m.
- A/B 1b)
- Wieviele Elemente enthält die Faltung einer Zahlenfolge der Länge 15
mit sich selbst? (B: Länge 22)
- L:
- Die Formel lautet n+m-1, also:
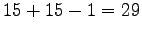 bzw.
bzw.
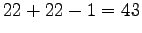 .
.
- A 1c)
- Wieviel freie Parameter enthält eine 3x3 Matrix für
die Festlegung einer Transformation in der Ebene in homogenen Koordinaten
und welches ist deren Bedeutung?
- L:
- Von den 9 Parametern sind 4 für die 2x2 Matrix und 2
für die Translation frei, also total 6,
die restlichen 3, in der letzten Zeile sind fest.
- B 1c)
- Welche Parameter einer 4x4 Matrix für
die Festlegung einer Transformation im Raum in homogenen Koordinaten
sind a priori festgelegt und auf welche Werte?
- L:
- In der untersten Zeile sind
 bis
bis 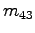 auf 0
und
auf 0
und 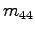 auf 1 festgelegt.
auf 1 festgelegt.
- A/B 1d)
- Aus den Matrizen R(4x3) ,
M(4x4) und dem (3x1)-Vektor v, sowie
deren Transponierten R', M', v' sollen 4 legale und 2 illegale
Matrizenprodukt-Zweierkombinationen gefunden werden (z.B. R*M), wobei die
Angabe legal oder illegal dazu zu schreiben ist.
Produkte mit gleichen Buchstaben, wie M*M oder v'*v sollen nocht vorkommen.
(B: R(5x3), M(5x5), v(3x1) , - 3 legale, 3 illegale)
- L:
- A/B: Legal - M*R, M'*R, R'*M', R'*M, R*v, v'*R'
- A 2)
- Bestimmen Sie
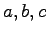 in der Matrix
in der Matrix 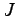 so dass gilt:
so dass gilt:
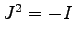 (
(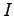 ist die Einheitsmatrix)!
ist die Einheitsmatrix)!
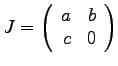
- L:
- a=0,( b=-1, c=1) oder (b=1, c=-1)
- B 2)
- Bestimmen Sie
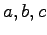 in der Matrix
in der Matrix 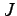 so dass gilt:
so dass gilt:
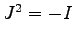 (
( ist die Einheitsmatrix)!
ist die Einheitsmatrix)!

- L:
- c=0,( a=-1, b=1) oder (a=1, b=-1)
A/B:
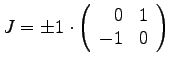
- A/B 3)
- Die nebenstehende Spirale hat in Polarkoordinaten die
Formel
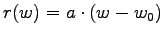 . Finden Sie
. Finden Sie 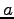 und
und 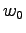 und geben Sie die Matlab Befehle an zum Zeichnen dieser Spirale! (Beachten
Sie dass die Spirale sich linksdrehend öffnet.)
und geben Sie die Matlab Befehle an zum Zeichnen dieser Spirale! (Beachten
Sie dass die Spirale sich linksdrehend öffnet.)
- L:
- A:
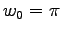 und
und
 (Radien-Zunahme um 2 bei Winkel-Abnahme um 2*
(Radien-Zunahme um 2 bei Winkel-Abnahme um 2* )
)
B: 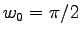 und
und
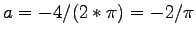
A: t = pi: -pi/200:-6*pi
xpt = -t/pi .* cos(t-pi)
ypt = -t/pi .* sin(t-pi)
B: t = pi/2: -pi/200:-6*pi
xpt = -2*t/pi .* cos(t-pi/2)
ypt = -2*t/pi .* sin(t-pi/2)
A/B: plot(xpt,ypt)
- A/B 4)
- Von den Punkten auf der x-Achse A
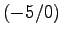 und B
und B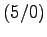 gehen
je drei Vektoren aus: AR, AS, AT, bzw. BR, BS, BT.
Von den Punkten R,S, T kennt man je die x-Koordinaten: -3, 1, 4 und weiss,
dass ihre y-Koordinaten positiv sind. Bestimmen Sie diese y-Koordinaten
aus der Bedingung, dass AS auf BS senkrecht steht und ebenso AR auf BR
und AT auf BT. Berechnen Sie anschliessend die Längen OR, OS, OT.
(O = Koordinaten-Ursprung)
gehen
je drei Vektoren aus: AR, AS, AT, bzw. BR, BS, BT.
Von den Punkten R,S, T kennt man je die x-Koordinaten: -3, 1, 4 und weiss,
dass ihre y-Koordinaten positiv sind. Bestimmen Sie diese y-Koordinaten
aus der Bedingung, dass AS auf BS senkrecht steht und ebenso AR auf BR
und AT auf BT. Berechnen Sie anschliessend die Längen OR, OS, OT.
(O = Koordinaten-Ursprung)
(B: A(-10/0), B(10/0) )
- L:
- Das Skalarprodukt AP*BP muss 0 sein für P=R,S,T,
dies ergibt die Formel
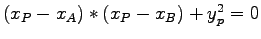 , also
, also
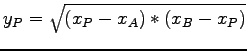 , das ist der altbekannten Höhensatz
für rechtwinklige Dreiecke.
, das ist der altbekannten Höhensatz
für rechtwinklige Dreiecke.
Die Werte für y ergeben: 4, 4.899, 3 (B: 6, 9.798, 8)
Die Distanzen OP sind alle gleich (Thaleskreis) A: 5 , B: 10.
- A/B 5)
- Suchen Sie die Gesamt-Transformations-Matrix,
in homogenen Koordinaten, welche die Punkte der Ebene um den
Drehpunkt (8/8) um 180
 dreht und testen Sie das Resultat
an den drei Punkten (8/10) (8/8) und (8/9) [besser (9/8)]!
dreht und testen Sie das Resultat
an den drei Punkten (8/10) (8/8) und (8/9) [besser (9/8)]!
(B: Drehpunkt (6/6), Punkte (6/8) (6/6) und (6/7) [besser (7/6)]).
- L:
-
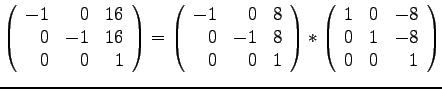
Transformierte Punkte: (8/6) (8/8) (8/7) [(7/8)]
B: analog mit 6 statt 8, 12 statt 16.
- A/B 6)
- Stellen Sie die Matrizengleichungen zum Lösen des folgenden
Gleichungssystems auf:
Eine Kleinfirma hatte 1999 total 5 Mio SFr. Brutto-Einnahmen.
Die Brutto-Einnahmen aus Italien und Österreich zusammen
entsprechen denjenigen von Deutschland. Die Netto- Einnahmen
aus Deutschland betragen wegen den Betriebskosten einer
Aussenstelle von 250'000 SFr. nur 1/4 der Brutto-Einnahmen
aus der Schweiz.
Die Speditionskosten nach Italien betragen 50'000 SFr.,
damit sind die Netto-Einnahmen aus Italien gleich wie diejenigen
aus Deutschland.
(B: total 10 Mio, Betrieb D 500'000, Spedition I 100'000, = alles *2 )
- L:
-
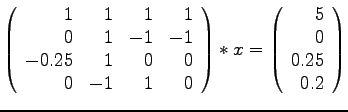












Nächste Seite: SS 2001 - Nachprüfung
Aufwärts: Sommersemester 2001
Vorherige Seite: Sommersemester 2001
Inhalt
2012-03-21
 in der Matrix enthaltenen Zahlen plus die
2 Dimensionszahlen n und m.
in der Matrix enthaltenen Zahlen plus die
2 Dimensionszahlen n und m.
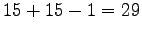 bzw.
bzw.
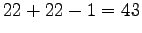 .
.
 bis
bis 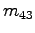 auf 0
und
auf 0
und 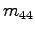 auf 1 festgelegt.
auf 1 festgelegt.
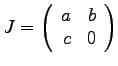

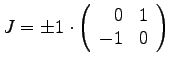
![\includegraphics[width=6cm, clip]{spirala}](img118.png)
![\includegraphics[width=6cm, clip]{spiralb}](img119.png)
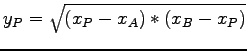 , das ist der altbekannten Höhensatz
für rechtwinklige Dreiecke.
, das ist der altbekannten Höhensatz
für rechtwinklige Dreiecke.