FS 09 - Lösung zur Prüfung 1, R-G-B-Y, 28. April 2009

R   Ingenieurmathematik Prüfung 1 28.April2009
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Die komplexe Zahlenfolge zv = [i 1 -i] ergibt beim Zeichnen einen Pfeil nach rechts. Mit welcher komplexen Zahl z müssen Sie zv multiplizieren, damit der Pfeil plot(z*zv) nach unten in die -Im(z) Richtung zeigt?

L1a)

Multiplizieren mit -i = exp(-i*pi/2) dreht 90 Grad im Uhrzeigersinn.

1b)

Bestimmen Sie die Zahlen n und m so, dass die folgendende Matrixmultiplikation legal ist: A(3xn)*B(5x3)*C(mx2).  Geben Sie auch die Dimension der Resultates an.

L1b)

n=5 , m = 3, ABC ist 3x2

1c)

Geben Sie die Inverse der Matrix R = [0.707 -0.707 ; 0.707 0.707] an und benützen Sie dabei die Tatsache, dass R orthogonal ist.
Geben Sie auch die Methode an, mit der Sie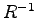 $R^{-1}$ bestimmt haben.

L1c)

R = [0.707 0.707 ; -0.707 0.707], transponieren

1d)

Welche Komponente des Vektors x wird beim Rückwärts-Einsetzen im nxn System R*x=y zuerst bestimmt und wie lautet die besonders einfach aufzulösende erste Gleichung, aus welcher man sie berechnen kann?

L1d)

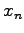$x_n$ aus $R_{nn} \cdot x_n = y_n$

2)

Suchen Sie die speziellen Permutations/Auswahlmatrizen $Pl$ und $Pr$, so dass die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!

$${ \left( \begin{array}{rrrrr} a_4 & a_2 & 0 & a_5 & 0 \\ d... ..._2 & e_3 & e_4 & e_5 \end{array} \right) \cdot Pr ~=~ Pl \cdot A \cdot Pr }$$

L2)

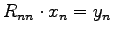
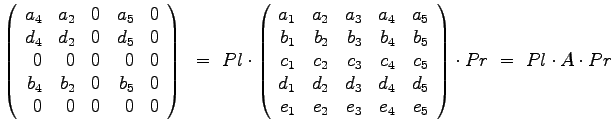
 Asel = [1 0 0 0 0; ...
         0 0 0 1 0; ...
         0 0 0 0 0; ...
         0 1 0 0 0; ...
         0 0 0 0 0] * iwmat(5) * ...
        [0 0 0 0 0
         0 1 0 0 0 
         0 0 0 0 0
         1 0 0 0 0
         0 0 0 1 0]

3)

Suchen sie alle komplexen Lösungen $z_k$ der Gleichung

$$z^7 + 128i = 0$$

L3)

zk = 2 * exp( i*(3*pi/14+k*2*pi/7) )
k=0:6; z = 2* exp(j*(3*pi/14+k*2*pi/7)) ; z.^7

4)

Die vierseitige Pyramide $A({-8}/{-8}/0)$ $B({8}/{-8}/0)$ $C({8}/{8}/0)$ $D({-8}/{8}/0)$ $S(0/0/10)$ wird mit einer Ebene geschnitten, welche durch die Punkte $B$, $C$ und $H(0/0/6)$ geht. Berechnen Sie die Durchstosspunkte Pd und Pa der Kanten DS und AS und damit die Schnittfigur B-C-Pd-Pa. Beweisen Sie, dass die Schittfigur ein Trapez ist, indem Sie zeigen, dass Pd-Pa parallel zu BC ist.

4)

%%%  R:
A = [-8 -8 0]' ; B = [8 -8 0]' ; C = [8 8 0]' ; D = [-8 8 0]' ; 
S = [0 0 10]'; H = [0 0 6]'
v = C-B , w = H-B   % v = [0 16 0]' , w = [-8 8 6]'
N = cross(v,w)      % N = [96 0 128]'
en = N/norm(N) , dkrit = en'*B  % en = [0.6 0 0.8]' ; dkrit = 4.8
%  en'*( [0 0 10] + la*[-8 -8 -10]) - dkrit = 0
%   la = (dkrit - en'*[0 0 10]')/(en'*[8 -8 -10]')
    lad = (dkrit - en'*[0 0 10]')/(en'*[-8 8 -10]')
Pd =  [0 0 10]' + lad*[-8 8 -10]'; % lad = 0.25 , Pd = [-2 2 7.5]  
Pdo = Pd'
%   
    laa = (dkrit - en'*[0 0 10]')/(en'*[-8 -8 -10]')
Pa =  [0 0 10]' + laa*[-8 -8 -10]'; % laa = 0.25 , Pa = [-2 -2 7.5]
Pao = Pa'
dP = (Pd-Pa)' , dB = (C-B)'
%  Winkel (  Pd-Pa , C-B )
w = acos((Pd-Pa)'*(C-B)/norm(Pd-Pa)/norm(C-B))

5)

In der Matrix C sind die L- und die R-Matrix zusammengepackt: auf- und oberhalb der Diagonalen befinden sich die Elemente der R-Matrix und ``echt'' unterhalb der Diagonalen stehen die Elemente der L-Matrix.
Erstellen Sie eine MATLAB-Funktion, welche eine C-Matrix als Eingangsparameter erhält und daraus die darin enthaltene R-Matrix rekonstruiert.

L5)

function Rbk = runpack(Comb)
%  function Rbk = runpack(Comb)
%   extract R- Part from L and R in Comb packed together
  [nz,ns] = size(Comb);
  Rbk = zeros(nz);
  for spa = 1:ns
    for zei = 1:spa
      Rbk(zei,spa) = Comb(zei,spa);
    end
  end

6)

Geben Sie die Teilmatrizen und die Gesamt-Transformations-Matrix an für die 2D homogene Koordinatentransformation, welche das rechtwinklige Dreieck ABC ($A(0/0)$, $B(10/0)$, $C(5/5)$) um $180^{\mathrm{o}}$  um den Mittelpunkt seiner Hypotenuse AB dreht. Geben Sie auch die Ecken des transformierten Dreiecks an.

L6)

A = [0 0 1]' ; B = [10 0 1]'; C = [5 5 1]';
M = (A+B)/2        %  [5 0 1]'
Tz = eye(3); Tz(1:2,3) = -M(1:2)
Tb = eye(3); Tb(1:2,3) = M(1:2)
R = eye(3); R(1:2,1:2) = [-1 0; 0 -1]
Dro = [A B C A]
Tt = Tb*R*Tz   % [-1 0 10; 0 -1 0; 0 0 1]
Drt = Tt*Dro   % [ 10 0 5 10; 0 0 -5 0; 1 1 1 1]