- 1a)
- Wie nennt man eine Matrix für welche gilt:
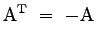 ?
?
- L1a)
- antisymmetrisch
- 1b)
- Wieviele Nullen darf eine nxn Eliminationsmatrix höchstens
enthalten wenn am Ort an dem in der bearbeiteten Matrix
eine Null erzeugt werden soll noch keine
Null steht?
- L1b)
- n*n-n-1, alle Diagonalelemente Eins, Eliminationsfaktor
verschieden von Null
- 1c)
- Geben Sie eine 4x4 Turm-Matrix an, welche bei Multiplikation
von links die erste und dritte Zeile der rechts stehenden Matrix vertauscht.
- L1c)
0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 1- 1d)
- Welche Wirkung hat die fest vorgeschriebene unterste Zeile mit den Werten
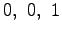 in der Matrix der 2D homogenen Koordinatentransformation
auf die zu transformierenden Vektoren?
in der Matrix der 2D homogenen Koordinatentransformation
auf die zu transformierenden Vektoren?
- L1d)
- Damit wird erreicht, dass jeder transformierte Vektor
wieder zuunterst eine Eins aufweist und daher weiter transformiert werden kann.
w = pi/2 + ( 0:2*pi/17:2*pi) x = 5*cos(w); y = 5*sin(w); plot(x,y,'g'); axis equal; hold on plot([-6 6],[0 0],'k'); plot([0 0], [-6 6],'k'); hold off
t = 0:pi/40:4*pi z = 0.5*exp(j*t)+ t; plot(z); hold on; axis equal plot([ pi/2+0.5*j 5*pi/2+0.5*j ],'og') plot([3*pi/2-0.5*j 7*pi/2-0.5*j ],'or') hold off
C = [-4 0 0]'; B = [0 4 0]'; D = [0 -4 0]'; S = [0 0 4]'; MBS = (B+S)/2 , MDS = (D+S)/2 % MBS = [0 2 2]; MDS = [0 -2 2]; n = cross(MDS-C, MBS-C), en = n/norm(n) % n = [-8 0 16]', en = [-0.4472 0 0.8944]' dkrit = en'*C % dkrit = 1.7889 % en'* OP - en'* OV = en'* OP - dkrit = [-0.4472 0 0.8944]*OP - 1.7889 = 0 distS = en'*S - dkrit % distS = 1.7889 (= dkrit Symmetrie!) eup = [0 0 1]', w = acos(eup'*en), wg = w*180/pi % w = 0.4636 ; wg = 26.56 Grd
Rur = [6 12 12 6 6; 0 0 4 4 0; 1 1 1 1 1]; Tz = [1 0 -6; 0 1 -2; 0 0 1] M = [-1 0 0; 0 -1 0; 0 0 1] Tb = [1 0 6; 0 1 2; 0 0 1] TT = Tb*M*Tz % = [1 0 12; 0 1 4; 0 0 1] Rtr = TT*Rur % =[ 6 0 0 6 6; 4 4 0 0 4; 1 1 1 1 1] plot(Rur(1,:),Rur( 2,:)); hold on; axis equal plot(Rtr(1,:),Rtr( 2,:)); hold off
x = 0:0.02:1; y = x; [xg,yg] = meshgrid(x,y); f = (2*xg.^3 - 3*xg.^2 +1) .* (-2*yg.^3 + 3*yg.^2) ; contour3(xg,yg,f,30); axis equal
