- 1a)
- Geben Sie eine 4x4 Matrix
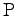 an, welche bei
Multiplikation von rechts her
an, welche bei
Multiplikation von rechts her
 die erste und die dritte Spalte von
die erste und die dritte Spalte von 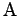 miteinander vertauscht!
miteinander vertauscht!
- L 1a)
[0 0 1 0 ; 0 1 0 0 ; 1 0 0 0; 0 0 0 1 ]- 1b)
- Geben Sie eine 3x3 Matrix, verschieden von der Einheitsmatrix an,
welche gleich ist wie ihre eigene Inverse!
- L 1b)
[-1 0 0 ; 0 1 0 ; 0 0 1 ], Diagonal mit 1
1
- 1c)
- Geben Sie die Buchstabengruppe an, mit der ein MATLAB-plot-Befehl
eine durchgezogene blaue Linie mit stehenden Kreuzchen als Markern erzeugt!
- L 1c)
- '+-b'
- 1d)
- Wie viele Lösungen gibt es bei einem linearen Gleichungssystem
der Dimension 4x4, falls es lösbar ist und der Rang der
Matrix 3 beträgt?
- L 1d)
- Singulär, lösbar, also unendlich viele Lösungen.
function A = antisympart(M)
% A = antisympart(M)
% extrahiert antisymmetrischen Teil von M
% in oberen Dreiecksbereich
A = 0*M; [nzei, nspa] = size(M);
if nzei == nspa
for zei = 1:nspa
for spa = zei+1:nspa
A(zei,spa) = (M(spa,zei) - M(zei,spa))/2;
end
end
end
a) den Punkt
b) den Punkt
Geben Sie ein MATLAB-Skript an, mit welchem die Kurve a) rot und die Kurve b) schwarz als 3D Kurve gezeichnet werden.
% Schraubenlinie a) wa = (0:0.01:1)*pi; za = 5*cos(wa); ya = -5*sin(wa) ; xa = wa*2/(2*pi); plot3(xa, ya, za, 'r' ); axis equal; hold on % Schraubenlinie b) wb = (1:-0.01:0)*pi; zb = 5*cos(wb); yb = -5*sin(wb) ; xb = 2- wb*2/(2*pi); plot3(xb, yb, zb, 'k' ); hold off
I) Spiegelung an der zur y-Achse parallelen Geraden durch den Mittelpunkt des Rechtecks
II) Spiegelung an der zur x-Achse parallelen Geraden durch den Mittelpunkt des Rechtecks.
% Rechteck Ru = [ 4 8 8 4 4; 0 0 6 6 0; 1 1 1 1 1]; % Spiegelung an der Geraden x = 6 Saz = [ 1 0 -6; 0 1 0; 0 0 1]; Ma = [-1 0 0; 0 1 0; 0 0 1]; Sag = [ 1 0 6; 0 1 0; 0 0 1]; Tta = Sag*Ma*Saz Ra = Tta* Ru % Spiegelung an der Geraden y= 3 Sbz = [ 1 0 0; 0 1 -3; 0 0 1]; Mb = [1 0 0; 0 -1 0; 0 0 1]; Sbg = [ 1 0 0; 0 1 3; 0 0 1]; Ttb = Sbg*Mb*Sbz Rb = Ttb* Ru
A = [4 0 0]'; B=[0 3 0]'; C= [-4 0 0]'; D=[0 -3 0]'; S= [0 0 3.2]'; Na = cross(A-S, B-S), ena = Na/norm(Na), dkrita = ena'*A Nb = cross(B-S, C-S), enb = Nb/norm(Nb), dkritb = enb'*B % Res: ena = [0.48 0.64 0.60]' , enb = [-0.48 0.64 0.60]' % test ena'*B, ena'*S, enb'*C, enb'*S % alle 1.92 % Winkel zwischen Einheitsvektoren, direkt Skalarprodukt win = 180/pi*acos(ena'*enb) % 57.3708 Grad
