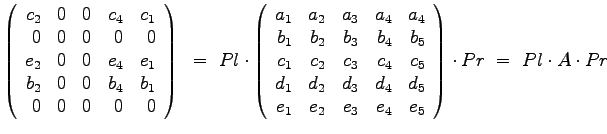


Nächste Seite: SS06 - Lösungen zur
Aufwärts: Sommersemester 2006
Vorherige Seite: SS 06 - Prüfung
Inhalt
Y
Ingenieurmathematik Prüfung 1
28.Juni2006
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe,
40 Pt. = N.6.
- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- 1a)
- Wieviele Begegnungen gibt es bei einer vollen Turnier-Runde mit
Hin- und Rückspielen von n Teilnehmern?
- 1b)
- Bestimmen Sie die zwei Resultate: Skalarprodukt der Vektoren
![$v = [1 ~ 1]'$](img1009.png) und
und ![$w = [1 ~ -1]'$](img1010.png) , sowie das Produkt der komplexen Zahlen
, sowie das Produkt der komplexen Zahlen
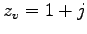 und
und 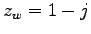 . Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
. Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
- 1c)
- Warum ist die Formel der Kramer'schen Regel für die praktische
Lösung von grösseren linearen Gleichungssystemen ungeeignet?
- 1d)
- Mit welchen MATLAB Befehlen erreicht man, dass die Grafik
in einem quadratischen Feld gezeichnet wird und dabei
die x-Werte zwischen
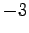 und
und 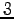 und die y-Werte
zwischen
und die y-Werte
zwischen 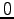 und
und  variieren?
variieren?
- 2)
- Suchen Sie die speziellen Permutations/Auswahlmatrizen
 und
und 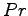 , so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
, so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
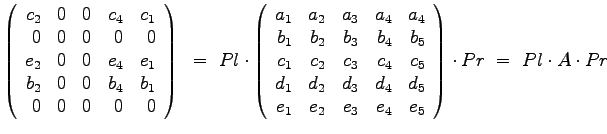
- 3)
- Suchen sie alle komplexen Lösungen der Gleichung
- 4)
- Gegeben ist der (nicht reguläre) Tetraeder ABCD
durch die Punkte
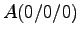 ,
, 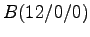 und
und
 ,
, 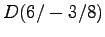 .
Geben Sie die Gleichung in der Hesse'schen Normalform an für die
mittelsenkrechte Ebene zur Strecke CD.
Berechnen Sie zusätzlich die Abstände aller Tetraeder-Ecken
von dieser Ebene.
.
Geben Sie die Gleichung in der Hesse'schen Normalform an für die
mittelsenkrechte Ebene zur Strecke CD.
Berechnen Sie zusätzlich die Abstände aller Tetraeder-Ecken
von dieser Ebene.
- 5)
- Suchen Sie die Teil-Transformationsmatrizen
und die Gesamt-Transformations-Matrix,
in homogenen Koordinaten der Ebene, welche das Quadrat ABCD
mit den Ecken
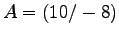 ,
, 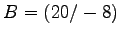 ,
, 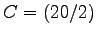 ,
, 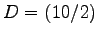 um
um
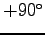 (im
Gegenuhrzeigersinnn) um die Ecke D dreht. Bestimmen Sie auch die
gedrehten Koordinaten ÃBCD.
(im
Gegenuhrzeigersinnn) um die Ecke D dreht. Bestimmen Sie auch die
gedrehten Koordinaten ÃBCD.
Geben Sie auch ein MATLAB-Skript an, das diese Transformation in
homogenen Koordinaten durchführt und das Urbild und Bild in eine
gemeinsame Grafik einzeichnet.
- 6)
- Suchen Sie die Darstellungen der beiden Schraubenlinien mit Achse auf der
y-Achse, welche
beide im Punkt (0/0/6) starten, wobei die rechtsdrehende Schraubenlinie
5 Umgänge in die
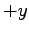 Richtung hat, und die linksdrehende ebensoviele in
die
Richtung hat, und die linksdrehende ebensoviele in
die 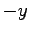 Richtung aufweist, beide mit einer Ganghöhe von 1.2.
Geben Sie ein MATLAB-Skript an, um diese in derselben Grafik
zu zeichnen.
Richtung aufweist, beide mit einer Ganghöhe von 1.2.
Geben Sie ein MATLAB-Skript an, um diese in derselben Grafik
zu zeichnen.












Nächste Seite: SS06 - Lösungen zur
Aufwärts: Sommersemester 2006
Vorherige Seite: SS 06 - Prüfung
Inhalt
2012-03-21
![$v = [1 ~ 1]'$](img1009.png) und
und ![$w = [1 ~ -1]'$](img1010.png) , sowie das Produkt der komplexen Zahlen
, sowie das Produkt der komplexen Zahlen
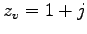 und
und 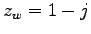 . Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
. Daraus sehen Sie, dass das Skalarprodukt und
die komplexe Multiplikation prinzipiell verschieden sind.
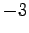 und
und 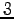 und die y-Werte
zwischen
und die y-Werte
zwischen 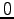 und
und  variieren?
variieren?